In this post, we’ll be discussing the use of several methods to find the volume of solid of revolution (VOSOR) around slant axis (besides the $x$-axis and $y$-axis). A problem of this type is quite uncommon - for that reason, this post is written to shed light on this subject matter.
Method 1: Pappus’ Centroid Theorem
Theorem 1.1 The second part of Pappus’ Centroid Theorem states that
he volume $V$ of a solid of revolution generated by rotating a plane figure $R$ about an external axis is equal to the product of the area $A$ of $R$ and the distance $d$ traveled by the geometric centroid of $F$.
\[V = Ad\]
Example 1.2 Find the volume of solid generated by revolving the region $R$ bound by the curves $x = \sqrt{-y}$ and $y = x^2 - 4x$ around the axis $y=x$ (see Figure 1).
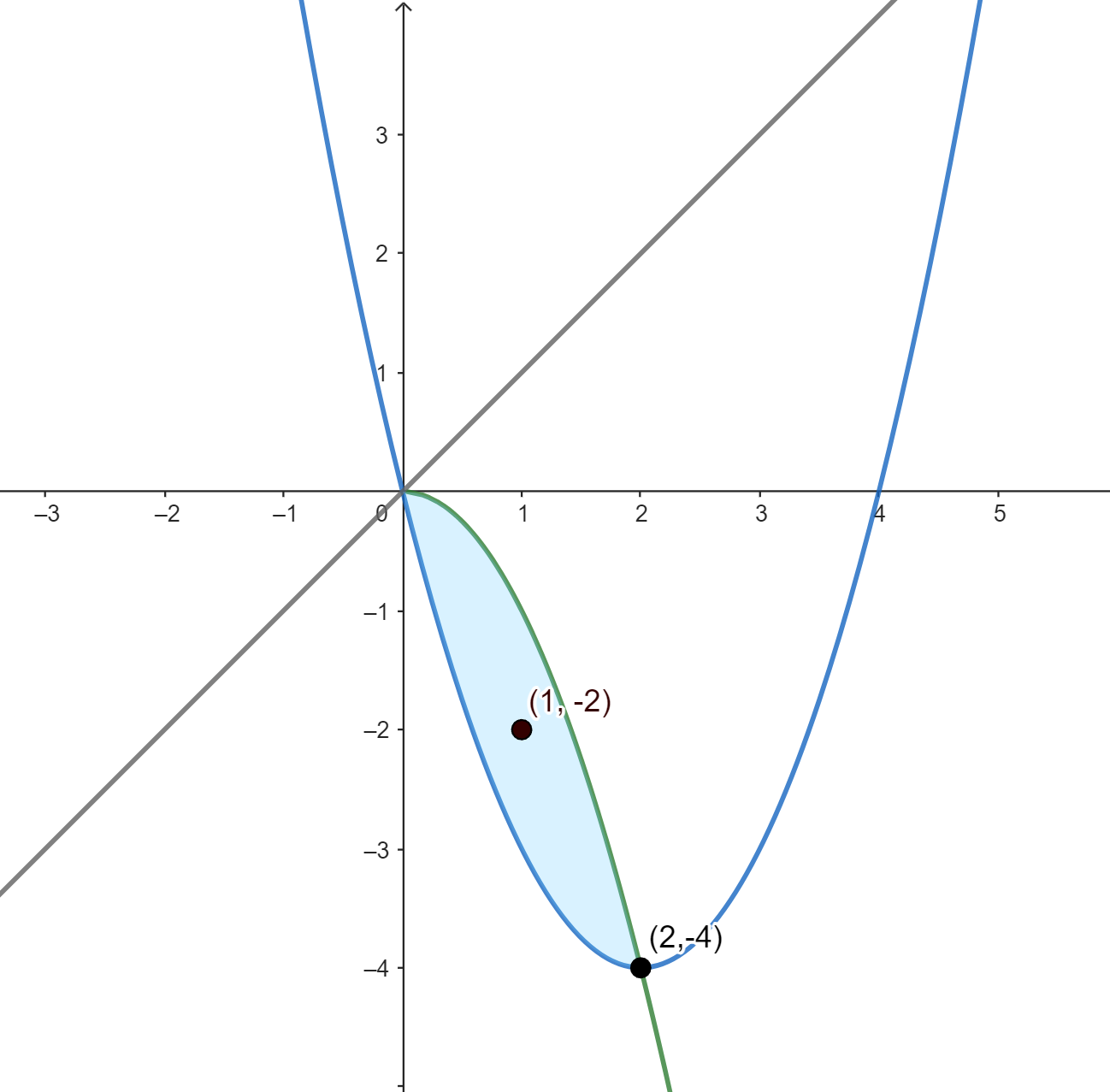
Finding the value of $s$ should be a relatively straightforward task. The hard part, however, involves knowing what $d$ is. Since the solid is generated from a revolution around an axis, we know that $d = 2\pi r$, where $r$ is the perpendicular distance between the centroid and the line $y=x$.
Definition 1.3 Let $(\overline{x}, \overline{y})$ be the coordinates of the centroid of the lamina.
By definition,
\[\overline{x} = \dfrac{M_y}{m}\]
and
\[\overline{y} = \dfrac{M_x}{m},\]
where $m$ denotes the mass of the lamina, $M_x$ and $M_y$ are the moments about the $x$-axis and the $y$-axis respectively.
Definition 1.4 Noting the density of a particular point $(x,y)$ on the lamina $R$ is given by $\rho(x,y)$, we shall find the values of $m, M_x$ and $M_y$ using the following formulae:
\[m = \int \int_R \rho(x,y)\,dA\]
\[M_x = \int \int_R y\rho(x,y)\,dA\]
\[M_y = \int \int_R x\rho(x,y) dA\]
Since the density function $\rho$ is not given, we can assume that the lamina has uniform density and assign $\rho(x,y) = 1$.
\[\begin{aligned}
m &= \int \int_R \rho(x,y)\,dA \\
&= \int^{x=2}_{x=0}\int^{y=-x^2}_{y=x^2-4x}\,dy\,dx \\
&= \int^{x=2}_{x=0} 4x - 2x^2 \,dx \\
&= \left[\left.2x^2 - \frac{2}{3}x^3\right|^{x=2}_{x=0}\right] \\
&= \frac{8}{3}
\end{aligned}\]
\[\begin{aligned}
M_x &= \int \int_R y\rho(x,y)\,dA \\
&= \int^{x=2}_{x=0}\int^{y=-x^2}_{y=x^2-4x}y\,dy\,dx \\
&=\int_{x=0}^{x=2}\left[\left.\frac{y^2}{2}\right|^{y=-x^2}_{y=x^2-4x}\right] \, dx \\
&= \frac{1}{2}\int^2_0 8x^3 - 16x^2 \,dx \\
&= -\frac{16}{3} \\
\end{aligned}\]
\[\begin{aligned}
M_y &= \int \int_R x\rho(x,y)\,dA \\
&= \int^{x=2}_{x=0}x\int^{y=-x^2}_{y=x^2-4x}\,dy\,dx \\
&=\int_{x=0}^{x=2}x(4x-2x^2) \, dx \\
&= \int^2_0 4x^2 - 2x^3 \,dx \\
&= \frac{8}{3}\\
\end{aligned}\]
Hence, $\overline{x} = \dfrac{8/3}{8/3} = 1$ and $\overline{y} = \dfrac{-16/3}{8/3} = -2$.
The distance of the $(\overline{x},\overline{y})$ from the line $y=x$ is $\dfrac{\mid 1-(-2) \mid}{\sqrt{1^2+(-1)^2}} = \dfrac{3\sqrt{2}}{2}.$
Owing to the fact that the lamina has uniform density, the area of the lamina is equal to $m$.
Finally, $V = Ad = \left(\dfrac{8}{3}\right)\left(2\pi \cdot \dfrac{3\sqrt{2}}{2}\right) = \boxed{8\pi\sqrt{2}}$
Method 2: Riemann Sum
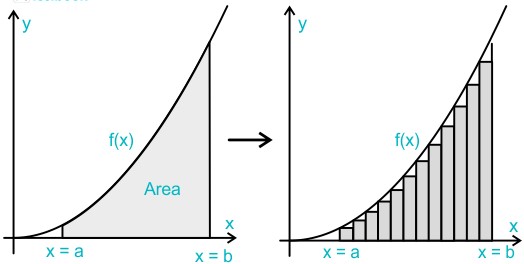
This method uses the same concept involved in defining a Riemann integral (with $n$ partitions of width $\Delta x$):
\[A = \lim_{\Delta x \to 0}\sum_{i=0}^{n-1}f(x_i)\Delta x = \int_a^b f(x)\,dx,\]
where $x_i = a + i\Delta x$ and $b = a + n\Delta x$.
Referring to Figure 2, the area of the shaded region is $A = \displaystyle \lim_{\Delta u \to 0}\sum_{i=1}^{n}L_i\Delta u$.
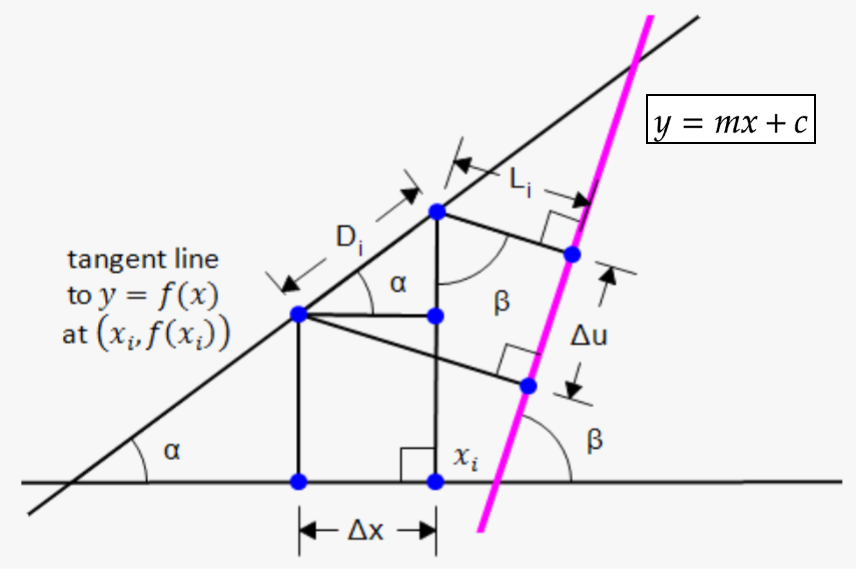
By drawing out the sketch above (Figure 3), we get to deduce $f’(x_i) = \tan{\alpha}$ and $m = \tan{\beta}$.
Then, $D_i = \dfrac{\Delta x}{\cos\alpha}$ and $\Delta u = D_i\cos(\beta - \alpha)$.
From the equations above,
\[\Delta u = \dfrac{\Delta x}{\cos\alpha}\cos(\beta - \alpha) = \dfrac{\Delta x}{\cos\alpha}(\cos\alpha\cos\beta + \sin\alpha\sin\beta) = \Delta x (\cos\beta + \tan\alpha\sin\beta)\]
Then, we need to express $\sin\beta$ and $\cos\beta$ in terms of $m$.
By drawing a right triangle and using $\tan \beta = m$, it is easy to see that
\[\sin \beta = \frac{m}{\sqrt{1+m^2}} \qquad \text{and} \qquad \cos \beta = \frac{1}{\sqrt{1+m^2}}\]
Thus, $\displaystyle \Delta u = \Delta x \left( \frac{1+mf’(x_i)}{\sqrt{1+m^2}}\right)$.
Then, we shall determine $L_i$. From the sketch,
\[L_i = (f(x_i) - (mx_i+c))\cos\beta = \frac{f(x_i) - mx_i-c}{\sqrt{1+m^2}}\]
Therefore, the area of region $R$ is
\[\begin{aligned}
\displaystyle A &=\lim_{\Delta u \to 0}\sum_{i=1}^{n}\left(\frac{f(x_i) - mx_i-c}{\sqrt{1+m^2}}\right)\Delta x \left( \frac{1+mf'(x_i)}{\sqrt{1+m^2}}\right) \\
&= \frac{1}{1+m^2}\lim_{\Delta u \to 0}\sum_{i=1}^{n}(f(x_i) - mx_i-c)(1+mf'(x_i))\Delta x\\
\therefore A &= \frac{1}{1+m^2}\int_a^b (f(x) - mx-c)(1+mf'(x))\,dx \end{aligned}\]
Similarly, the volume of the solid generated by revolving $R$ about $y=mx+b$ can be obtained by the following:
\[\begin{aligned}
V &= \lim_{\Delta u \to 0}\sum^n_{i=1}\pi L_i^2 \Delta u \\
&= \frac{1}{(1+m^2)^{3/2}}\int_a^b \pi(f(x) - mx-c)^2(1+mf'(x))\,dx \\
\end{aligned}\]
Using the formula above, we can quickly solve the following example.
Example 2.1 Find the volume of the solid generated by revolving the region $R$ bound by the curve $y = x^2$ and the line $y=x$
For this problem, $f(x) = x^2 \implies f’(x) =2x$ and $m=1, c=0$.
The points of intersection are $(0,0)$ and $(1,1)$.
\[\begin{aligned}
V &= \frac{1}{(1+1^2)^{3/2}}\int^1_0 \pi(x^2-x)^2(1+(1)(2x)) \,dx \\
&= \frac{\pi}{2\sqrt{2}}\int^1_0 2x^5 -3x^4 + x^2\,dx \\
&= \frac{\pi\sqrt{2}}{4}\left[\frac{1}{3}x^6-\frac{3}{5}x^5+\frac{1}{3}x^3\right]^1_0 \\
&= \boxed{\frac{\pi\sqrt{2}}{60}}.
\end{aligned}\]
Method 3: Rotating the graph about the origin
Example 3.1 Suppose we had to find the volume of the solid generated by revolving the region $R$ bound by $y=x^2$ and and $y=x$.
While there are well-known methods to approach problems involving revolution about horizontal axes or vertical axes (e.g. Washer Method), it makes us wonder whether this notion can extended to any slant axes.
For that reason, why don’t we just rotate the entire Cartesian plane so that the slant axis ($y=x$ in our case) lies on the $x$-axis or the $y$-axis? (see Figure 4)
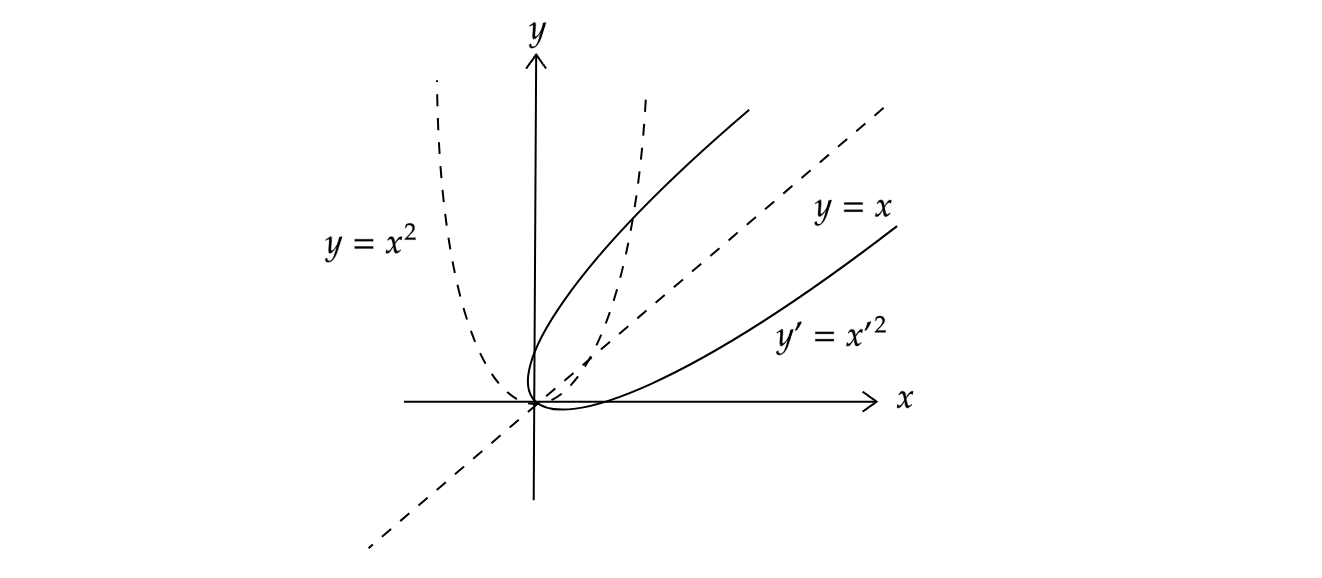
If we rotated $y=x^2$ 90° counterclockwise, we’d get $x = -y^2$.
If we rotated $y=x^2$ 180° counterclockwise, we’d get $y=-x^2$.
If we rotated $y=x^2$ 270° counterclockwise, we’d get $x=y^2$.
How about $45^{\circ}$? Or even $69^{\circ}$?
We shall utilise one of two common ways to perform the rotation.
Polar coordinates
We shall use a parametric form to express $x$ and $y$.
\(x = r\cos\theta \qquad \text{and} \qquad y = r\sin\theta\)
After rotating the Cartesian plane by $\alpha$ radians counterclockwise, the new parametric forms are:
\[x' = r\cos(\theta-\alpha) \qquad \text{and} \qquad y' = r\sin(\theta-\alpha)\]
When $y=x^2$ is expressed in the polar form, we obtain $r\sin\theta = r^2\cos^2\theta \iff r = \sec\theta \tan\theta$.
If we were to map the line $y=x$ onto the $x$-axis, this transformation would be equivalent to rotating the entire Cartesian plane by $\pi/4$ clockwise (or $-\pi/4$ counterclockwise).
\[x' = r\cos\left(\theta + \dfrac{\pi}{4}\right) = r\cos\left(\dfrac{\pi}{4}\right)\cos\theta - r\sin\left(\dfrac{\pi}{4}\right)\sin\theta = \dfrac{x-y}{\sqrt{2}}\]
\[y' = r\sin\left(\theta + \dfrac{\pi}{4}\right) = r\sin\left(\dfrac{\pi}{4}\right)\cos\theta + r\cos\left(\dfrac{\pi}{4}\right)\sin\theta = \dfrac{x+y}{\sqrt{2}}\]
After the rotation, $y’= (x’)^2$ becomes $\dfrac{x+y}{\sqrt{2}} = \left(\dfrac{x-y}{\sqrt{2}}\right)^2$.
A more straightforward way of rotating graphs is none other than applying a rotation matrix to a set of coordinates.
Let $\bf{x}$ be the position vector of a point on $y=x^2$.
Let \(\bf{M} := \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix}\) , which represents the rotation $\theta$ radians counterclockwise.
A graph is transformed by the following equation when $\theta = -\pi/4$:
\[\begin{aligned}
\bf{Mx} &= \bf{x'} \\
\begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} &= \begin{bmatrix} x' \\ y'\end{bmatrix} \\
\begin{bmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2}\end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} &= \begin{bmatrix} x' \\ y'\end{bmatrix}
\end{aligned}\]
This gives us $x’ = \dfrac{x-y}{\sqrt{2}}$ and $y’ = \dfrac{x+y}{\sqrt{2}}$. Since $y’=(x’)^2$, then $\dfrac{x+y}{\sqrt{2}} = \left(\dfrac{x-y}{\sqrt{2}}\right)^2$.
The new curve intercepts the $x$-axis at $x=0$ and $x=\sqrt{2}$.
Since our desired volume is $\displaystyle V= \int^{x=\sqrt{2}}_{x=0}\pi y^2\,dx$, we have to solve for $y$.
\[\dfrac{x+y}{\sqrt{2}} = \left(\dfrac{x-y}{\sqrt{2}}\right)^2 \implies y^2 - (2x+\sqrt{2})y + x^2-x\sqrt{2}=0\]
Using the quadratic formula,
\[y=\frac{1}{2}\left(2x+\sqrt{2}-\sqrt{2+8x\sqrt{2}}\right)\]
We’ve rejected the positive root since $y$ is always negative within our region $R$. Then, squaring both sides and expanding yields
\[y^2 = \frac{1}{4}\left(4x^2 + 12x\sqrt{2}+4 - 4x\sqrt{2+8x\sqrt{2}} - 2\sqrt{4+16x\sqrt{2}}\right)\]
Then, we define $I_1$ and $I_2$ as follows:
\[\begin{aligned}
I_1 &:= \int^{\sqrt{2}}_0 4x^2 + 12x\sqrt{2} + 4 \,dx \\
&= \left[\frac{4}{3}x^3 + 6x^2\sqrt{2}+4x\right]^{\sqrt{2}}_0 \\
&= \frac{56}{3}\sqrt{2} \\
\end{aligned}\]
\[I_2 := \int^{\sqrt{2}}_0 4x\sqrt{2+8x\sqrt{2}} + 2\sqrt{4+16x\sqrt{2}}\, dx\]
Let $u^2 = 2+8x\sqrt{2} \iff x = \dfrac{u^2 - 2}{8\sqrt{2}} \implies 2u \, du = 8\sqrt{2} \, dx \iff dx = \dfrac{u}{4\sqrt{2}}du$.
\[\begin{aligned} I_2 &= \int^{3\sqrt{2}}_{\sqrt{2}} \left(4\left(\frac{u^2 -2}{8\sqrt{2}}\right)u + 2u\sqrt{2}\right) \cdot \frac{u}{4\sqrt{2}}\,du \\
&= \int^{3\sqrt{2}}_{\sqrt{2}} \frac{1}{16}u^4 + \frac{3}{8}u^2 \, du \\
&= \left[\frac{1}{80}u^2 + \frac{1}{8}u^3\right]^{3\sqrt{2}}_{\sqrt{2}} \\
&= \frac{93}{5}\sqrt{2} \\
\end{aligned}\]
Our desired volume is $\displaystyle V= \int^{x=\sqrt{2}}_{x=0}\pi y^2\,dx = \frac{\pi}{4}(I_1 - I_2) = \frac{\pi}{4}\left(\frac{56}{3}\sqrt{2} - \frac{93}{5}\sqrt{2}\right) = \boxed{\frac{\pi\sqrt{2}}{60}}$.